Consumers' inflation expectations are very disperse; on household surveys, many people report long-run inflation expectations that are far from the Fed's 2% target. Are these people unaware of the target, or do they know it but remain unconvinced of its credibility? In another paper in the Journal of Macroeconomics, I provide some non-experimental evidence that public knowledge of the Fed and its objectives is quite limited. In this paper, we directly treat respondents with information about the target and about past inflation, in randomized order, and see how they revise their reported long-run inflation expectations. We also collect some information about their prior knowledge of the Fed and the target, their self-reported understanding of inflation, and their numeracy and demographic characteristics. About a quarter of respondents knew the Fed's target and two-thirds could identify Yellen as Fed Chair from a list of three options.I gave a 90 minute econ seminar today with the twin babies, both awake. Held one and audience passed the other around. A first in economics?— Carola Conces Binder (@cconces) September 28, 2017
As shown in the figure above, before receiving the treatments, very few respondents forecast 2% inflation over the long-run and only about a third even forecast in the 1-3% range. Over half report a multiple-of-5% forecast, which, as I argue in a recent paper in the Journal of Monetary Economics, is a likely sign of high uncertainty. When presented with a graph of the past 15 years of inflation, or with the FOMC statement announcing the 2% target, the average respondent revises their forecast around 2 percentage points closer to the target. Uncertainty also declines.
The results are consistent with imperfect information models because the information treatments are publicly available, yet respondents still revise their expectations after the treatments. Low informedness is part of the reason why expectations are far from the target. The results are also consistent with Bayesian updating, in the sense that high prior uncertainty is associated with larger revisions. But equally noteworthy is the fact that even after receiving both treatments, expectations are still quite heterogeneous and many still substantially depart from the target. So people seem to interpret the information in different ways and view it as imperfectly credible.
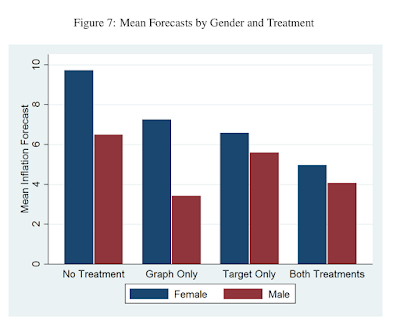
We look at how treatment effects vary by respondent characteristic. One interesting result is that, after receiving both treatments, the discrepancy between mean male and female inflation expectations (which has been noted in many studies) nearly disappears (see figure below).
There is more in the paper about how treatment effects vary with other characteristics, including respondents' opinion of government policy and their prior knowledge. We also look at whether expectations can be "un-anchored from below" with the graph treatment.